VIDEO

CONCLUSIÓN 

A través del tiempo una gran cantidad de personajes han dedicado su vida para contribuir con la realización de cálculos que ayuden y nos lleven a encontrar respuestas y resultados exactos para así descubrir el porque de los fenómenos y hechos en la historia humana. 

Unos de los puntos dentro de la matemática a resaltar seria las funciones trigonométricas son valores sin unidades que dependen de la magnitud de un ángulo. Se dice que un ángulo situado en un plano de coordenadas rectangulares está en su posición normal si su vértice coincide con el origen y su lado inicial coincide con la parte positiva del eje x.

Estas funciones fueron creadas a partir de la trigonometría plana y esférica para después ser perfeccionada y lograr lo que hoy llamamos Funciones Trigonométricas, es necesario dejar claro que es importante ya que forma parte de la matemáticas y que es fundamental en el desarrollo de algunas operaciones de cálculos para así obtener los resultados de los objetivos trazados.

TOMADO DE WIKIPEDIA

4) La cotangente de un ángulo es la relación entre la longitud del cateto adyacente y la del opuesto:

5) La secante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente:

6) La cosecante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto opuesto:

TOMADO DE WIKIPEDIA 

DEFINICIONES RESPECTO DE UN TRIANGULO RECTÁNGULO

Para definir las razones trigonométricas del ángulo: , del vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los sucesivo será:

• La hipotenusa (h) es el lado opuesto al ángulo recto, o lado de mayor longitud del triángulo rectángulo.
• El cateto opuesto (a) es el lado opuesto al ángulo .
• El cateto adyacente (b) es el lado adyacente al ángulo .

Todos los triángulos considerados se encuentran en el Plano Euclidiano, por lo que la suma de sus ángulos internos es igual a π radianes (o 180°). En consecuencia, en cualquier triángulo rectángulo los ángulos no rectos se encuentran entre 0 y π/2 radianes. Las definiciones que se dan a continuación definen estrictamente las funciones trigonométricas para ángulos dentro de ese rango:

1) El seno de un ángulo es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa:

El valor de esta relación no depende del tamaño del triángulo rectángulo que elijamos, siempre que tenga el mismo ángulo  , en cuyo caso se trata de triángulos semejantes.

2) El coseno de un ángulo es la relación entre la longitud del cateto adyacente y la longitud de la hipotenusa:

3) La tangente de un ángulo es la relación entre la longitud del cateto opuesto y la del adyacente:

TOMADO DE WIKIPEDIA 

Existen seis funciones trigonométricas básicas. Las últimas cuatro, se definen en relación de las dos primeras funciones, aunque se pueden definir geométrica mente o por medio de sus relaciones. Algunas funciones fueron comunes antiguamente, y aparecen en las primeras tablas, pero no se utilizan actualmente ; por ejemplo el ver seno (1 − cos θ) y la ex secante (sec θ − 1).

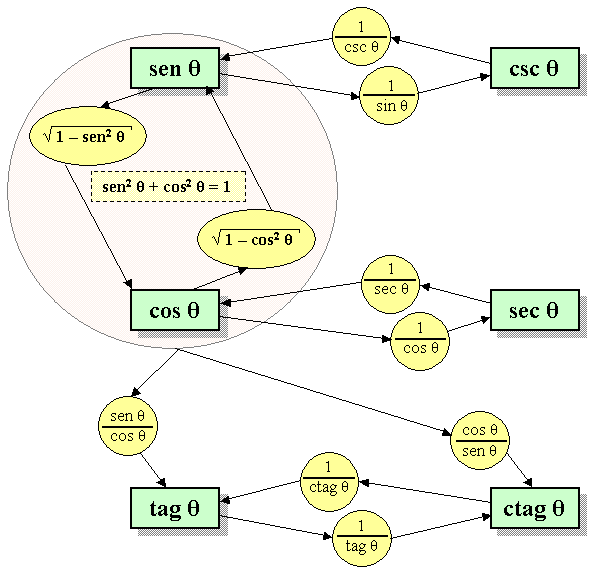
TOMADO DE WIKIPEDIA

CONCEPTOS BÁSICOS 

Las funciones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo asociado a sus ángulos. Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circunferencia unitaria (de radio unidad). Definiciones más modernas las describen como series infinitas o como la solución de ciertas ecuaciones diferenciales, permitiendo su extensión a valores positivos y negativos, e incluso a números complejos.

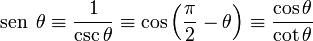
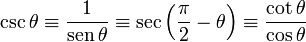
TOMADO DE WIKIPEDIA

DEFINICIÓN

En matemáticas, las funciones trigonométricas son las funciones establecidas con el fin de extender la definición de las razones trigonométricas a todos los números reales y complejos.

Las funciones trigonométricas son de gran importancia en física, astronomía, cartografía, náutica, telecomunicaciones, la representación de fenómenos periódicos, y otras muchas aplicaciones.

Todas las funciones trigonométricas de un ángulo θ pueden ser construidas geométrica mente en relación a una circunferencia de radio unidad de centro O.

TOMADO DE WIKIPEDIA

INTRODUCCIÓN

En términos generales, la trigonometría es el estudio de las funciones seno, coseno, tangente, cotangente, secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.

TOMADO DE WIKIPEDIA